【数Ⅰ】式の展開と因数分解④

この記事では、複２次式の解法を簡単にまとめた。

複２次式とは？

解法

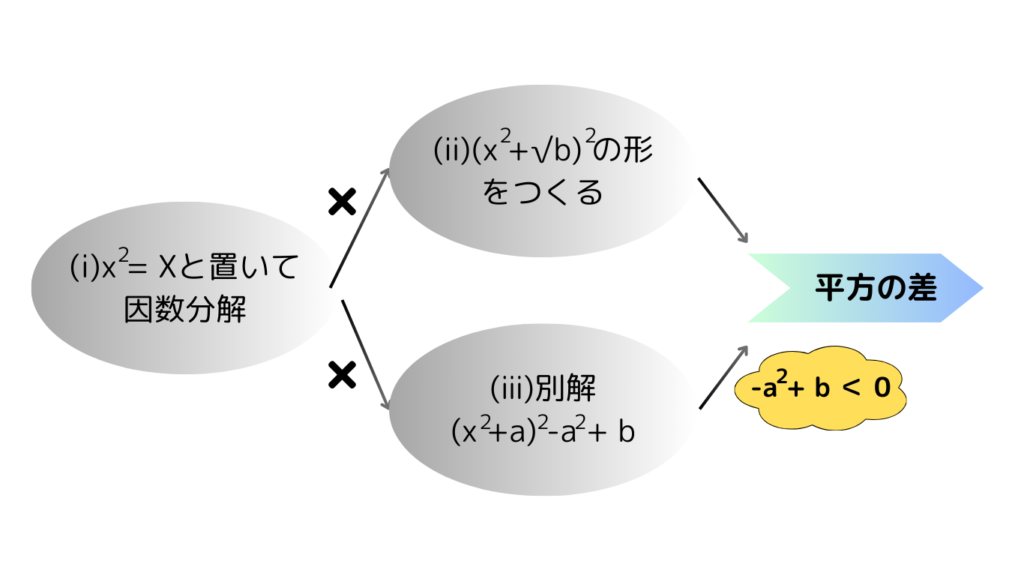
練習問題

$$(1) x^4-7x^2+1$$ $$ (2) x^4+5x^2+9$$ $$ (3) 25x^4-6x^2+1$$

上のチャート表を参考に解いてみよう！

※今回は（ⅰ）で完結する問題は割愛する。

解答・解説

(1) (ⅱ)x⁴の項と定数項で平方完成すると、

$$(x^2+1)^2-2x^2-7x^2$$

$$= (x^2+1)^2-(3x)^2$$

$$= (x^2+1+3x)(x^2+1-3x) $$

※別解　(ⅲ)平方完成をすると、

$$(x^2-\frac{7}{2})^2-(\frac{7}{2})^2+1$$

$$=(x^2-\frac{7}{2})^2-\frac{45}{4}$$

$$=(x^2-\frac{7}{2})^2-(\frac{3\sqrt5}{2})^2$$

$$=(x^2-(\frac{7}{2}-\frac{3\sqrt5}{2}))(x^2-(\frac{7}{2}+\frac{3\sqrt5}{2})) $$

$$=(x+\sqrt(\frac{7}{2}-\frac{3\sqrt5}{2}))(x-\sqrt(\frac{7}{2}-\frac{3\sqrt5}{2}))(x+\sqrt(\frac{7}{2}+\frac{3\sqrt5}{2}))(x-\sqrt(\frac{7}{2}+\frac{3\sqrt5}{2})) $$

(２) (ⅱ)x⁴の項と定数項で平方完成すると、

$$(x^2+3)^2-6x^2+5x^2$$

$$=(x^2+3)^2-x^2$$

$$=(x^2+3+x)(x^2+3-x)$$

※別解　(ⅲ)平方完成をすると、

$$(x^2+\frac{5}{2})^2-(\frac{5}{2})^2+9$$

$$(x^2-\frac{7}{2})^2+(\frac{11}{4})^2$$

となり、第二項が正となるため、この解法は不適。

(1) (ⅱ)x⁴の項と定数項で平方完成すると

$$(5x^2+1)^2-10x^2-6x^2$$

$$=(5x^2+1)^2-(4x)^2$$

$$=(5x^2+1+2x)(5x^2+1-2x)$$

※別解　与式を25でくくり、a=-3/25, b=1/25 とすると、-a²+b＜0となるので別解は存在する。興味がある人はやってみるとよい。

さいごに

別解を実際に計算してみた方もいるかもしれないが、実用的ではないことは明らかだ。

ただ、このような解法もあるということを頭の片隅においておくと、いいことがあるかも…

複２次式 → x⁴の項と定数項で平方完成

これだけは押さえておいていただきたい。